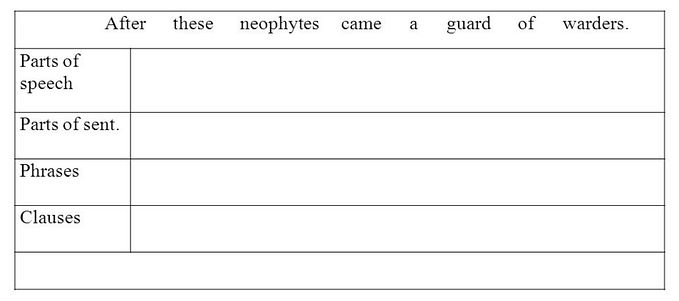
Spell Check and Levenshtein Distance

5 min readJun 22, 2023

Spell check is an amazing feature that I can’t imagine going without. We’ve gotten so used to it that we forget how often it comes into play everyday. After all, can you imagine typing a query in a search engine with absolutely correct spelling?! Just one mistyped word or letter is all takes to throw all the search engine results into disarray! And yet, that never happens. Spell check is automatically applied each time we use a search engine, and thank god for that!

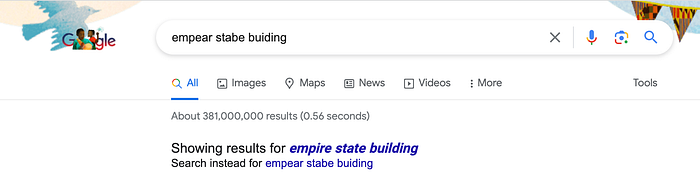
From a surface level perspective, spell check is split up into two phases: recognizing incorrect spellings and finding the correct spelling for the intended word. Recognizing incorrect spellings is technically an easy programming task since every word in an search query can be checked against all words in a dictionary, but realistically speaking that approach is computation heavy (over 600k English word-forms!) and time intensive so there are most likely algorithms for just recognizing incorrect spellings. The more difficult task I’d say is determining the intended word, which modern programs have incorporated to not only analyze the misspelled word but also the context in which it is used. Doing so has also allowed for grammar correction.

So spell check is meant to find incorrect words, but if you think about it there’s different types of incorrect words with some harder to detect than others. One type of error is a misspelling, but this is relatively easy to do. The less obvious alternative is an incorrect word itself, despite correct spelling. How do you instruct a computer to find a word that is spelled correctly, but used incorrectly in a sentence? It might be easy for humans, but it doesn’t seem that easy to teach computers.

Thus, the phases of spell check are to recognize errors, determine a set of intended words / corrections, and lastly to rank the set of possible words in a manner that returns the most likely / probable word to match the originally intended word.

Levenshtein Distance

Levenshtein Distance (LD) is a method for measuring the similarity between two strings. It calculates the distance or amount of alterations necessary to transform one word into another. Consider word #1 to be “lock” and word #2 to be “chalk”. The goal is to transform word #1 into word #2 using the minimum number of operations possible. If you think about it, a singular alteration or operation can only be an insertion, deletion, or substitution. Levenshtein Distance is a way of optimizing transformation operations which minimizes the distance between word #1 and word #2. In terms of spell check, if we consider that even an incorrectly spelled word contains elements that are to some extent correct, then Levenshtein Distance can help to at the very least narrow down the list of possible intended words to a relatively small amount.

There are 5 rules / possibilities / cases to consider while constructing a LD solution.

1. Case — When the respective characters of both words are the same, no operation is necessary

Consider the words “book” and “back”, in which both “b” and “k” are the correct letters in the right position. The LD = 2 because 2 simple substitutions will transform “book” into “back”. However, it is not necessary for the original word to be the same length as the target word, from which positioning complications occur which is why indexed elements are compared starting from the end for both convenience and efficiency. The first rule is as below:

# X ==> word 1 - original
# Y ==> word 2 - target
# i ==> current index looping through X
# j ==> current index looping through Y

# RULE 1
if(X[i] == Y[j]): # NOTE: This process must start from one direction - the back
  # then discard ith element of X and jth element of Y b/c doesn't affect LD
  X = X[:i]
  Y = Y[:j]

2. Case — When the original word or target word is empty, LD = non-empty word

If the original or target is empty, then it is a simple case of insertion or deletion respectively.

# RULE 2
if(len(X) == 0 or len(Y) == 0):
  LD = max(len(X), len(Y))

3. Possibility — Insertion

An insertion is only done when the target word is longer than the original word. Consider a letter that is added to the end of the original word such that it matches the end of the target. The LD += 1, and the last letter of both the original and targets words are irrelevant.

# Insertion case possibility
X += "s" # NOTE: insertion present, so last letter no longer matters
# target ==> ducks
# original ==> ____ => ____s

# j ==> last index of target word

# NOTE: letter cut off of target
findLev(X,Y) = findLev(X, Y[:j]) + 1 #this 1 accounts for insertion operation

4. Possibility — Deletion

Similarly, deletion is only present when the original word is longer than the target word. If a character is deleted from the original word, then LD += 1 and the edit distance of the original word minus the last letter in comparison to the target word must be found.

# Deletion case possibility
X = X[:len(X)-1]

# i==> last index of original word

# NOTE: last letter cut off original
findLev(X,Y) = findLev(X[:i], Y) + 1 #this 1 accounts for deletion operation

5. Possibility — Substitution

Consider a substitution of the last character of the original word. This is an operation in which LD += 1, but since the last characters of the original and target match, they are now irrelevant.

# Substitution case possibility
# target ==> ____s
# original ==> _____ => ____s

# i ==> last index of original word
# j ==> last index of target word

# NOTE: last letter cut off both original and target
findLev(X,Y) = findLev(X[:i], Y[:j]) + 1 #substitution operation accounted for

The Solution

The fastest solution is using matrices. However, I will demonstrate the Levenshtein Distance solution recursively, albeit at the cost of memory space and time.

Matrices Ex.

The first rule acts as a base case, while the second rule takes precedence in case the the first rule’s preconditions are not activated. Finally, since I am using recursion all the possible combinations of insertion, deletion, and substitution are accounted for while looking for the minimum Levenshtein distance / edit distance.

The code is as follows.

def lev(i, j):
    if(min(i, j) == 0):
        return max(i, j)
    if(word1[i - 1] == word2[j - 1]):
        return lev(i - 1, j - 1)
    return min(lev(i - 1, j) + 1, lev(i, j - 1) + 1, lev(i - 1,j - 1) +1)

word1 = input("Enter word 1:\t")
word2 = input("Enter word 2:\t")

print(lev(len(word1), len(word2)))

-----------------------------------OUTPUT--------------------------------------

Enter word 1:   cobs
Enter word 2:   foobar
Leveshtein Distance: 4

Sources

https://www.enjoyalgorithms.com/blog/edit-distance

https://www.codingninjas.com/codestudio/library/levenshtein-distance-nlp